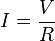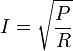Blogger para discussão e troca de informações sobre o curso técnico em eletrotécnica - CA CCI - Patos
relogio
terça-feira, 5 de junho de 2012
Leis de Kirchhoff (videos)
Segue alguns videos sobre Lei de Kirchhoff (teoria e exercícios), não esquecendo que a prova do professor Almir sera neste sábado dia 09 / 06
Leis de Kirchhoff
As Leis de Kirchhoff são empregadas em circuitos elétricos mais complexos, como por exemplo circuitos com mais de uma fonte de resistores estando em série ou em paralelo. Para estuda-las vamos definir o que são Nós e Malhas:
-> Nó: é um ponto onde três (ou mais) condutores são ligados.
-> Malha: é qualquer caminho condutor fechado.
Analisando a figura 1, vemos que os pontos a e d são nós, mas b, c, e e f não são. Identificamos neste circuito 3 malhas definidas pelos pontos: afed, adcb e badc.
Primeira lei de Kirchhoff (lei dos nós)
Em qualquer nó, a soma das correntes que o deixam(aquelas cujas apontam para fora do nó) é igual a soma das correntes que chegam até ele. A Lei é uma conseqüência da conservação da carga total existente no circuito. Isto é uma confirmação de que não há acumulação de cargas nos nós.
Segunda lei de Kirchhoff (lei das malhas)
A soma algébrica das forças eletromotrizes (f.e.m) em qualquer malha é igual a soma algébrica das quedas de potencial ou dos produtos iR contidos na malha.
Aplicando as leis de Kirchhoff
Exemplo 1: A figura 1 mostra um circuito cujos elementos têm os seguintes valores:
E1=2,1 V, E2=6,3 V, R1=1,7 Ώ, R2=3,5 Ώ. Ache as correntes nos três ramos do circuito.
Solução: Os sentidos das correntes são escolhidos arbitrariamente. Aplicando a 1ª lei de Kirchhoff (Lei dos Nós) temos:
i1 + i2 = i3
ou
Se percorrermos a malha adef no sentido horário temos:
ou
Resolvendo o sistema temos que:
i1 = 0,82A
i2 = -0,4A
i3 = 0,42A
Os sinais das correntes mostra que escolhemos corretamente os sentidos de i1 e i3, contudo o sentido de i2 está invertido, ela deveria apontar para cima no ramo central da figura 1.
Exemplo 2: Qual a diferença de potencial entre os pontos a e d da figura 1?
Solução: Pela Lei da Malhas temos:
Observe que se não alterarmos o sentido da corrente i2, teremos que utilizar o sinal negativo quando for feito algum cálculo com essa corrente.
segunda-feira, 4 de junho de 2012
Associação de capacitores
Os capacitores, assim como os resistores, podem ser associados em série, paralelo ou misto. Esses são elementos de circuito elétrico que tem como principal função o armazenamento de cargas elétricas. Essas associações têm como objetivo obter a capacitância desejada.
Capacitores em Série
Nesse tipo de associação, os capacitores são ligados da seguinte forma: a armadura positiva de um capacitor é ligada com a armadura negativa do outro capacitor e assim sucessivamente. Para determinar a capacitância equivalente de uma associação de dois ou mais capacitores utilizamos a seguinte relação matemática:
Capacitores em Paralelo
Em paralelo, as placas positivas dos capacitores são ligadas entre si, bem como as negativas. Para determinar a capacitância equivalente utiliza-se a seguinte equação matemática, veja:
Capacitores
Capacitor (português brasileiro) ou condensador (português europeu) é um componente que armazena energia num campo elétrico, acumulando um desequilíbrio interno de carga elétrica.
Em outubro de 1745, Ewald Georg von Kleist, descobriu que uma carga poderia ser armazenada, conectando um gerador de alta tensão eletrostática por um fio a uma jarra de vidro com água, que estava em sua mão. A mão de Von Kleist e a água agiram como condutores, e a jarra como um dielétrico (mas os detalhes do mecanismo não forram identificados corretamente no momento). Von Kleist descobriu, após a remoção do gerador, que ao tocar o fio, o resultado era um doloroso choque. Em uma carta descrevendo o experimento, ele disse: "Eu não levaria um segundo choque para o reino de França". No ano seguinte, na Universidade de Leiden, o físico holandês Pieter van Musschenbroek inventou um capacitor similar, que foi nomeado de Jarra de Leyden.
Daniel Gralath foi o primeiro a combinar várias jarras em paralelo para aumentar a capacidade de armazenamento de carga. Benjamin Franklin investigou a Jarra de Leyden e "provou" que a carga estava armazenada no vidro, e não na água como os outros tinham suposto. Ele também adotou o termo "bateria", posteriormente aplicada a um aglomerados de células eletroquímicas.
Jarras de Leyden foram utilizados exclusivamente até cerca de 1900, quando a invenção do wireless (rádio) criou uma demanda por capacitores padrão, e o movimento constante para frequências mais altas necessitavam de capacitores com baixa indutância.
No início capacitores também eram conhecidos como condensadores, um termo que ainda é utilizado atualmente. O termo foi usado pela primeira vez por Alessandro Volta em 1782, com referência à capacidade do dispositivo de armazenar uma maior densidade de carga elétrica do que um condutor normalmente isolado.
Exemplos de capacitores.
A escala principal é dada em centímetros.
Vídeos sobre Leis de Ohm e Resistores + exercícios
Ola pessoal segue alguns videos sobre Leis de Ohm, Resistores e exercícios diversos
Lei de Ohm
A lei de ohm é uma teoria que compreende os estudos realizados com a resistência elétrica determinando que a resistência é a razão da tensão sobre uma carga elétrica dividido pela corrente elétrica que está passando por ela.
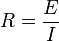
Essa teoria pode ser expressa pela fórmula da lei de Ohm da seguinte maneira: R= E/ I onde, R é resistência elétrica, E a tensão elétrica e I a corrente elétrica. Através dessa fórmula matemática podemos calcular a resistência elétrica de um circuito.
Podemos trabalhar matematicamente a fórmula para extrair os valores de outras grandezas como tensão elétrica E=R.I ou ainda a calcularmos a intensidade da corrente elétrica com a fórmula I= E/R. Dessa maneira podemos conseguir os valores para podermos dimensionar um circuito.
Se calcularmos os valores das grandezas da eletricidade podemos saber a intensidade da corrente elétrica de um circuito, então, podemos determinar o valor de um fusível de proteção, pode-se dimensionar um interruptor de acordo com os valores além de poder utilizar um condutor, que na maioria dos casos são fios de cobre, o mais dimensionado possível aos valores do circuito.
A potência elétrica também pode ser calculada através da fórmula P=E.I, pode-se trabalhar esta fórmula isolando E, e também o I.
A Lei de Ohm, assim designada em homenagem ao seu formulador Georg Simon Ohm, indica que a diferença de potencial (E) entre dois pontos de um condutor é proporcional à corrente elétrica (I).
Georg Simon Ohm
Quando essa lei é verdadeira num determinado resistor, este denomina-se resistor ôhmico ou linear. A resistência de um dispositivo condutor é dada pela fómula:
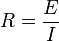
onde:
E é a diferença de potencial elétrico (ou tensão, ou ddp) medida em Volts
R é a resistência elétrica do circuito medida em Ohms
I é a intensidade da corrente elétrica medida em Ampères
Ohm
Essa teoria pode ser expressa pela fórmula da lei de Ohm da seguinte maneira: R= E/ I onde, R é resistência elétrica, E a tensão elétrica e I a corrente elétrica. Através dessa fórmula matemática podemos calcular a resistência elétrica de um circuito.
Podemos trabalhar matematicamente a fórmula para extrair os valores de outras grandezas como tensão elétrica E=R.I ou ainda a calcularmos a intensidade da corrente elétrica com a fórmula I= E/R. Dessa maneira podemos conseguir os valores para podermos dimensionar um circuito.
Se calcularmos os valores das grandezas da eletricidade podemos saber a intensidade da corrente elétrica de um circuito, então, podemos determinar o valor de um fusível de proteção, pode-se dimensionar um interruptor de acordo com os valores além de poder utilizar um condutor, que na maioria dos casos são fios de cobre, o mais dimensionado possível aos valores do circuito.
A potência elétrica também pode ser calculada através da fórmula P=E.I, pode-se trabalhar esta fórmula isolando E, e também o I.
--> Conhecendo-se duas das grandezas envolvidas na Lei de Ohm, é fácil calcular a terceira:
A potência P, em Watts, dissipada num resistor, na presunção de que os sentidos da corrente e da tensão são aqueles assinalados na figura, é dada por
Logo, a tensão ou a corrente podem ser calculadas a partir de uma potência conhecida:
Outras relações, envolvendo resistência e potência, são obtidas por substituição algébrica:
Assinar:
Comentários (Atom)